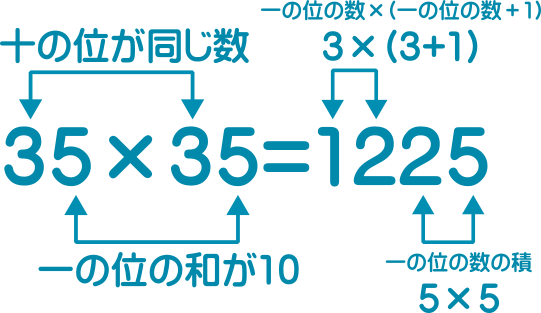今日はインド式算数を紹介したいと思います。
日本の算数では九九を覚えますが、インドでは\(19\times19\)まで覚えたり、工夫して暗算で計算できるようにするそうです。
さらに2桁×2桁の掛け算はできる限り暗算できるようにするようです。
それでは、その計算方法を紹介していきたいと思います。
十の位が同じ数で、一の位の和が10になる場合
十の位が同じ数で、一の位の和が10となる2数の積は、下の例題のように求めることができます。
例題

[証明]
\(a,\;b,\;c\;\)を一桁の自然数、かつ、\(\;b+c=10\;\)とする。
2桁の数を\(10a+b,\;10a+c\;\)とすると
$$\begin{align}(10a+b)(10a+c)&=100a^2+10a(b+c)+bc\\&=100a^2+100a+bc\\&=100a(a+1)+bc\end{align}$$
[証明終]
類題1

類題2
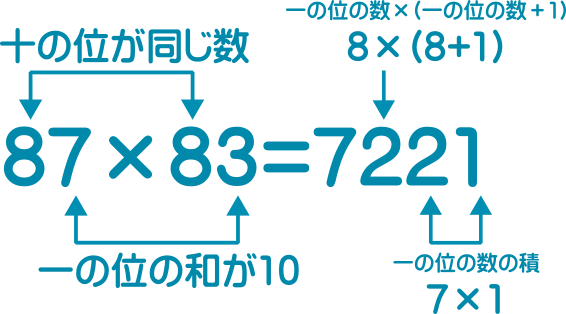
類題4